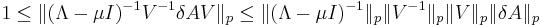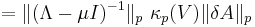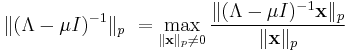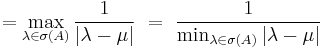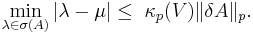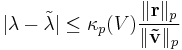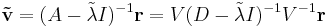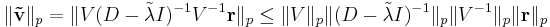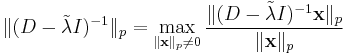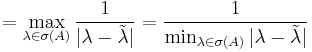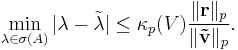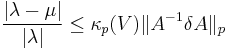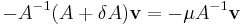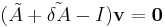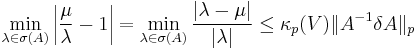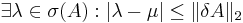Bauer–Fike theorem
In mathematics, the Bauer–Fike theorem is a standard result in the perturbation theory of the eigenvalue of a complex-valued diagonalizable matrix. In its substance, it states an absolute upper bound for the deviation of one perturbed matrix eigenvalue from a properly chosen eigenvalue of the exact matrix. Informally speaking, what it says is that the sensitivity of the eigenvalues is estimated by the condition number of the matrix of eigenvectors.
Contents |
Theorem (Friedrich L. Bauer, C.T.Fike – 1960)
Let 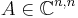 be a diagonalizable matrix, and
be a diagonalizable matrix, and 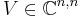 be the non singular eigenvector matrix such that
be the non singular eigenvector matrix such that 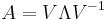 . Be moreover
. Be moreover  an eigenvalue of the matrix
an eigenvalue of the matrix 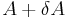 ; then an eigenvalue
; then an eigenvalue 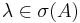 exists such that:
exists such that:
where 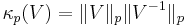 is the usual condition number in p-norm.
is the usual condition number in p-norm.
Proof
If 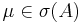 , we can choose
, we can choose 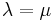 and the thesis is trivially verified (since
and the thesis is trivially verified (since 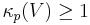 ).
).
So, be 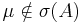 . Then
. Then 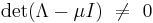 .
.  being an eigenvalue of
being an eigenvalue of 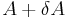 , we have
, we have 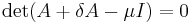 and so
and so
and, since 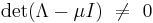 as stated above, we must have
as stated above, we must have
which reveals the value −1 to be an eigenvalue of the matrix 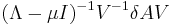 .
.
For each consistent matrix norm, we have 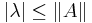 , so, all p-norms being consistent, we can write:
, so, all p-norms being consistent, we can write:
But 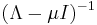 being a diagonal matrix, the p-norm is easily computed, and yields:
being a diagonal matrix, the p-norm is easily computed, and yields:
whence:
The theorem can also be reformulated to better suit numerical methods. In fact, dealing with real eigensystem problems, one often has an exact matrix  , but knows only an approximate eigenvalue-eigenvector couple, (
, but knows only an approximate eigenvalue-eigenvector couple, (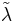 ,
,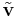 ), and needs to bound the error. The following version comes in help.
), and needs to bound the error. The following version comes in help.
Theorem (Friedrich L. Bauer, C.T.Fike – 1960) (alternative statement)
Let 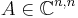 be a diagonalizable matrix, and be
be a diagonalizable matrix, and be 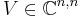 the non singular eigenvector matrix such as
the non singular eigenvector matrix such as 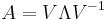 . Be moreover (
. Be moreover (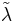 ,
,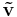 ) an approximate eigenvalue-eigenvector couple, and
) an approximate eigenvalue-eigenvector couple, and 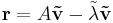 ; then an eigenvalue
; then an eigenvalue 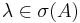 exists such that:
exists such that:
where 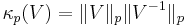 is the usual condition number in p-norm.
is the usual condition number in p-norm.
Proof
We solve this problem with Tarık's method: m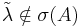 (otherwise, we can choose
(otherwise, we can choose 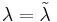 and theorem is proven, since
and theorem is proven, since 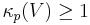 ). Then
). Then 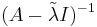 exists, so we can write:
exists, so we can write:
since  is diagonalizable; taking the p-norm of both sides, we obtain:
is diagonalizable; taking the p-norm of both sides, we obtain:
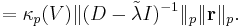
But, since 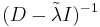 is a diagonal matrix, the p-norm is easily computed, and yields:
is a diagonal matrix, the p-norm is easily computed, and yields:
whence:
The Bauer–Fike theorem, in both versions, yields an absolute bound. The following corollary, which, besides all the hypothesis of Bauer–Fike theorem, requires also the non-singularity of A, turns out to be useful whenever a relative bound is needed.
Corollary
Be 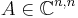 a non-singular, diagonalizable matrix, and be
a non-singular, diagonalizable matrix, and be 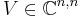 the non singular eigenvector matrix such as
the non singular eigenvector matrix such as 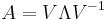 . Be moreover
. Be moreover  an eigenvalue of the matrix
an eigenvalue of the matrix 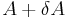 ; then an eigenvalue
; then an eigenvalue 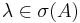 exists such that:
exists such that:
(Note: 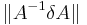 can be formally viewed as the "relative variation of A", just as
can be formally viewed as the "relative variation of A", just as 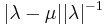 is the relative variation of λ.)
is the relative variation of λ.)
Proof
Since μ is an eigenvalue of (A+δA) and 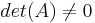 , we have, left-multiplying by
, we have, left-multiplying by 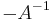 :
:
that is, putting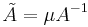 and
and 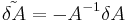 :
:
which means that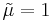 is an eigenvalue of
is an eigenvalue of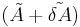 , with
, with 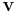 eigenvector. Now, the eigenvalues of
eigenvector. Now, the eigenvalues of 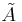 are
are 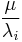 , while its eigenvector matrix is the same as A. Applying the Bauer–Fike theorem to the matrix
, while its eigenvector matrix is the same as A. Applying the Bauer–Fike theorem to the matrix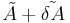 and to its eigenvalue
and to its eigenvalue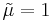 , we obtain:
, we obtain:
Remark
If A is normal, V is a unitary matrix, and 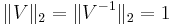 , so that
, so that 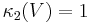 .
.
The Bauer–Fike theorem then becomes:
- (
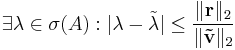 in the alternative formulation)
in the alternative formulation)
which obviously remains true if A is a Hermitian matrix. In this case, however, a much stronger result holds, known as the Weyl theorem.
References
- F. L. Bauer and C. T. Fike. Norms and exclusion theorems. Numer. Math. 2 (1960), 137–141.
- S. C. Eisenstat and I. C. F. Ipsen. Three absolute perturbation bounds for matrix eigenvalues imply relative bounds. SIAM Journal on Matrix Analysis and Applications Vol. 20, N. 1 (1998), 149–158
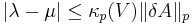
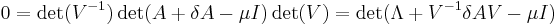
![=\det(\Lambda-\mu I)\det[(\Lambda-\mu I)^{-1}V^{-1}\delta AV %2BI]](/2012-wikipedia_en_all_nopic_01_2012/I/aed120d0be2c80d80202f68d325afe4e.png)
![\det[(\Lambda-\mu I)^{-1}V^{-1}\delta AV %2BI]=\ 0](/2012-wikipedia_en_all_nopic_01_2012/I/dcdd52e191a6acf313739de30a964b82.png)